Internship at SCK∙CEN in Mol, Belgium
Reported by Tymofii Khvan. Powered by FuseNet

From cylinders to dog-bones: Putting Tungsten to the Test
My internship was part of a project addressing the impact of neutron irradiation on mechanical properties of tungsten. In particular, my particular task was do a series of mechanical tensile tests under a different temperatures (RT – 600 ℃), analyze the geometry of deformed samples, perform data acquisition and reconstruct the engineering as well as the true stress-strain relationship. The true stress-strain is the real material parameter to be used for engineering finite element calculations. Two different types of samples were studied: cylindrical wires and rectangular so-called "dog bone" samples.
A stressful challenge
To achieve this goal, it was important to find an appropriate mathematical model to describe the behavior of these two types of specimen during plastic deformation. The main challenge was to identify a way of calculating “true stress – true strain” curves, while having only the final geometry of the broken samples rather than intermediate information on the evolution of the sample geometry. Application of the standard procedure to recover a stress-strain response would be incorrect because the diffuse necking begins shortly after the onset of the plastic deformation.
A successful estimation
To calculate the required true stress-strain the following approach was used. Firstly, the true strain was calculated directly by estimating the reduction of the cross-section area. Using this estimation the true stress could be calculated as well from the measured stress.
Experiments using Cylindrical samples
The estimation of cylindrical cross-section area was based on the geometrical parameters of the as-broken samples, which were inspected in the necking regions by optical microscopy.

Figure 1: Light optical microscopy measurement of cylindrical specimens.
We decided to consider the half-part of the broken specimen as a conical frustum. However, because of the small specimen’s size we have an uncertainty on optical measurements. Therefore the total strain was compared with the experimental data to double check the approach. To do this, the difference between the height of the conical frustum (broken half of specimen) and a cylinder with the same volume (part of specimen before experiment) was estimated. Then, the strain value in the fracture stress moment was calculated and compared with the experimental strain graph for each specimen. The best matching results were used for calculating the true stress – true strain curves, such as the example shown in figure 2.
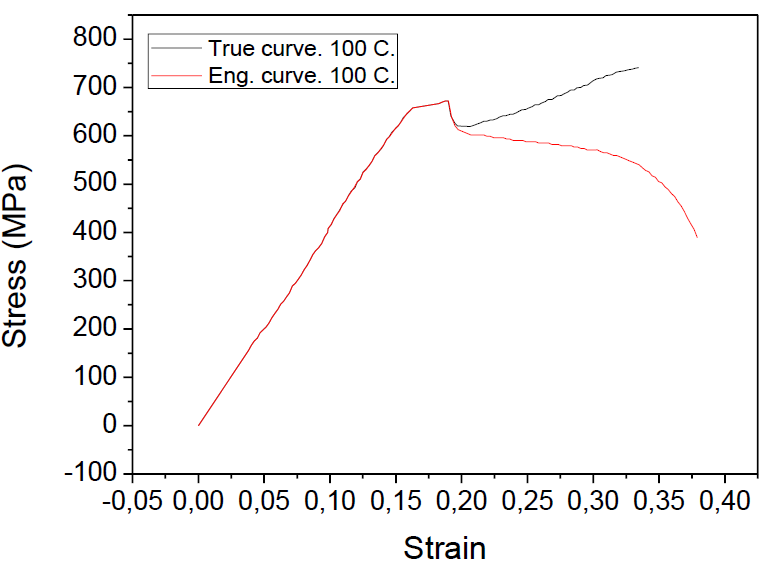
Figure 2: True and engineering stress-strain curves for one of the cylindrical wires.
Experiments using Rectangular samples
For rectangular samples we decided that the area reduction is going linearly and is split in three different regions:
- The first region holds for the part of curve from the beginning of experiment until the Yield stress point. Here we calculated the area reduction using Poisson’s ratio and found that the reduction is negligible in this elastic region. Therefore it was decided to not change the area value until the Yield stress point.
- The second region was used from the Yield stress point until the Ultimate tensile stress. Here the cross section area was calculated using the volume ratio between the Yield stress point and the Ultimate tensile stress point.
- The third region starts after the Ultimate tensile stress and extends to the Fracture stress. The Fracture stress areas were calculated from optical microscopy. Intermediate values were found by filling an interval between the Ultimate tensile stress area and Fracture stress area.

Figure 3: Light optical microscopy measurement of dog bone-type specimens.
To predict the measurement uncertainty we computed two true stress curves. The first one is for 0.0025 mm2 of measured area and the second one is for twice this value (the used uncertainty can be estimated in figure 3). This area value is average difference between the most suitable points for measuring the dimensions near the neck. After this, a polynomial fit of concatenate for each pair of calculated curves was performed using OriginPro. Figure 4 shows the obtained curves.
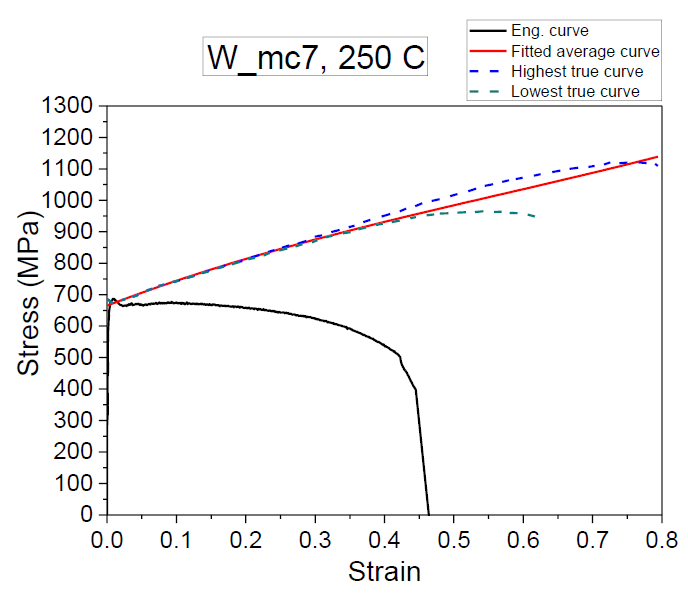
Figure 4: True and engineering curves for dog bone-type specimens.
Summary
A set of mechanical tests for bulk and wire tungsten samples was performed in the temperature range RT/250 °C – 600 °C. The deformed samples were characterized by light optical microscopy to extract the geometry in the necking region and reconstruct the true stress-strain curves. Because of this work we finished an important preparation stage for the tensile tests of tungsten specimens after neutron irradiation.
